AST로 구문 분석 게임 레벨 업하기!

원문 : Leveling Up One’s Parsing Game With ASTs - Vaidehi Joshi

컴퓨터 과학을 배우려는 이 여정을 시작하기 전에는 다른 방향으로 달려가고 싶다는 생각이 들게 하는 용어와 문구가 있었습니다.

하지만 저는 도망치는 대신에 아는 척하며 대화 중에 고개를 끄덕이며 누군가가 말하는 내용을 아는 척했고, 사실은 전혀 몰랐고 실제로는 그 슈퍼 무서운 컴퓨터 과학 용어™를 들었을 때 완전히 듣지 않았음에도 불구하고 알고 있는 척했습니다. 이 시리즈를 진행하는 동안 저는 많은 내용을 다룰 수 있었고 실제로 많은 용어가 훨씬 덜 무섭게 느껴졌습니다!

하지만 한동안 피하고 있던 큰 용어가 하나 있습니다. 지금까지는 이 용어를 들을 때마다 마비되는 기분이 들었습니다. 모임에서 일상적인 대화에서, 때로는 컨퍼런스 강연에서 이 용어가 등장하곤 했습니다. 그때마다 기계가 돌아가고 컴퓨터가 해독할 수 없는 코드 문자열을 뱉어내는 장면이 떠올랐지만, 주변 사람들은 모두 해독할 수 있어서 사실 무슨 일이 일어나고 있는지 모르는 것은 저뿐이었습니다(어떻게 이런 일이 일어났죠?!).

아마 저만 그런 느낌을 받은 것은 아닐 것입니다. 하지만 이 용어가 실제로 무엇인지 말씀드려야 할 것 같네요. 제가 지금 말씀드리는 것은 이해하기 어렵고 혼란스러워 보이는 추상 구문 트리(Abstract Syntax Tree), 줄여서 AST를 말하는 것이니 준비하세요. 수년간의 두려움 끝에 마침내 이 용어에 대한 두려움을 멈추고 도대체 이 용어가 무엇인지 진정으로 이해하게 되어 기쁩니다.

이제 추상 구문 트리의 근원을 정면으로 마주하고 구문 분석 게임의 레벨을 높일 때입니다!

구체적인 것에서 추상적인 것으로

모든 좋은 탐구는 탄탄한 기초에서 시작되며, 이 구조를 이해하기 위한 우리의 임무는 당연히 정의에서 시작되어야 합니다!

추상 구문 트리(일반적으로 AST라고만 함)는 실제로는 구문 분석 트리(Parse Tree)의 단순화되고 압축된 버전에 지나지 않습니다. 컴파일러 설계의 맥락에서 “AST”라는 용어는 구문 트리와 같은 의미로 사용됩니다.

우리는 종종 구문 트리(그리고 그 구성 방식)를 구문 분석 트리와 비교하여 생각하는데, 이는 이미 꽤 익숙한 개념입니다. 구문 분석 트리는 코드의 문법 구조를 포함하는 트리 데이터 구조, 즉 코드 ‘문장’에 나타나는 모든 구문 정보를 포함하고 프로그래밍 언어 자체의 문법에서 직접 파생된다는 것을 알고 있습니다.

반면 추상 구문 트리는 구문 분석 트리가 포함할 수 있는 상당량의 구문 정보를 무시합니다.

반면 AST에는 소스 텍스트 분석과 관련된 정보만 포함되며, 텍스트를 구문 분석하는 동안 사용되는 다른 추가 콘텐츠는 건너뜁니다.

AST의 ‘추상성’에 초점을 맞추면 이러한 구분이 훨씬 더 이해가 되기 시작합니다.

구문 분석 트리는 문장의 문법 구조를 그림으로 표현한 것입니다. 다시 말해, 구문 분석 트리는 표현식, 문장 또는 텍스트가 정확히 어떻게 생겼는지를 나타낸다고 할 수 있습니다. 기본적으로 텍스트 자체를 직접 번역하는 것으로, 문장을 가져와 구두점부터 표현식, 토큰에 이르기까지 모든 작은 부분을 트리 데이터 구조로 변환합니다. 이는 텍스트의 구체적인 구문을 드러내기 때문에 구체적인 구문 트리(Concrete Syntax Tree) 또는 CST라고도 합니다. 이 구조를 설명할 때 구체적이라는 용어를 사용하는 이유는 트리 형식의 코드가 토큰 단위로 문법적으로 복사되어 있기 때문입니다.

그렇다면 무엇이 구체적이고 추상적인 것일까요? 추상 구문 트리는 구문 분석 트리처럼 표현식이 어떻게 생겼는지 정확히 보여주지 않습니다.

오히려 추상 구문 트리는 코드 ‘문장’ 자체에 의미를 부여하는 “중요한” 부분, 즉 우리가 정말로 신경 쓰는 부분을 보여줍니다. 구문 트리는 표현식의 중요한 부분, 즉 소스 텍스트의 추상화된 구문을 보여줍니다. 따라서 구체적인 구문 트리와 비교할 때 이러한 구조는 코드를 추상적으로 표현한 것이므로(어떤 면에서는 덜 정확합니다), 구문 트리라는 이름이 붙여진 것입니다.

이제 이 두 데이터 구조의 차이점과 코드를 표현하는 다양한 방법을 이해했으니, 컴파일러에서 추상 구문 트리가 어디에 적합한지 질문해 볼 필요가 있습니다. 먼저 지금까지 컴파일 프로세스에 대해 알고 있는 모든 것을 상기해 봅시다.

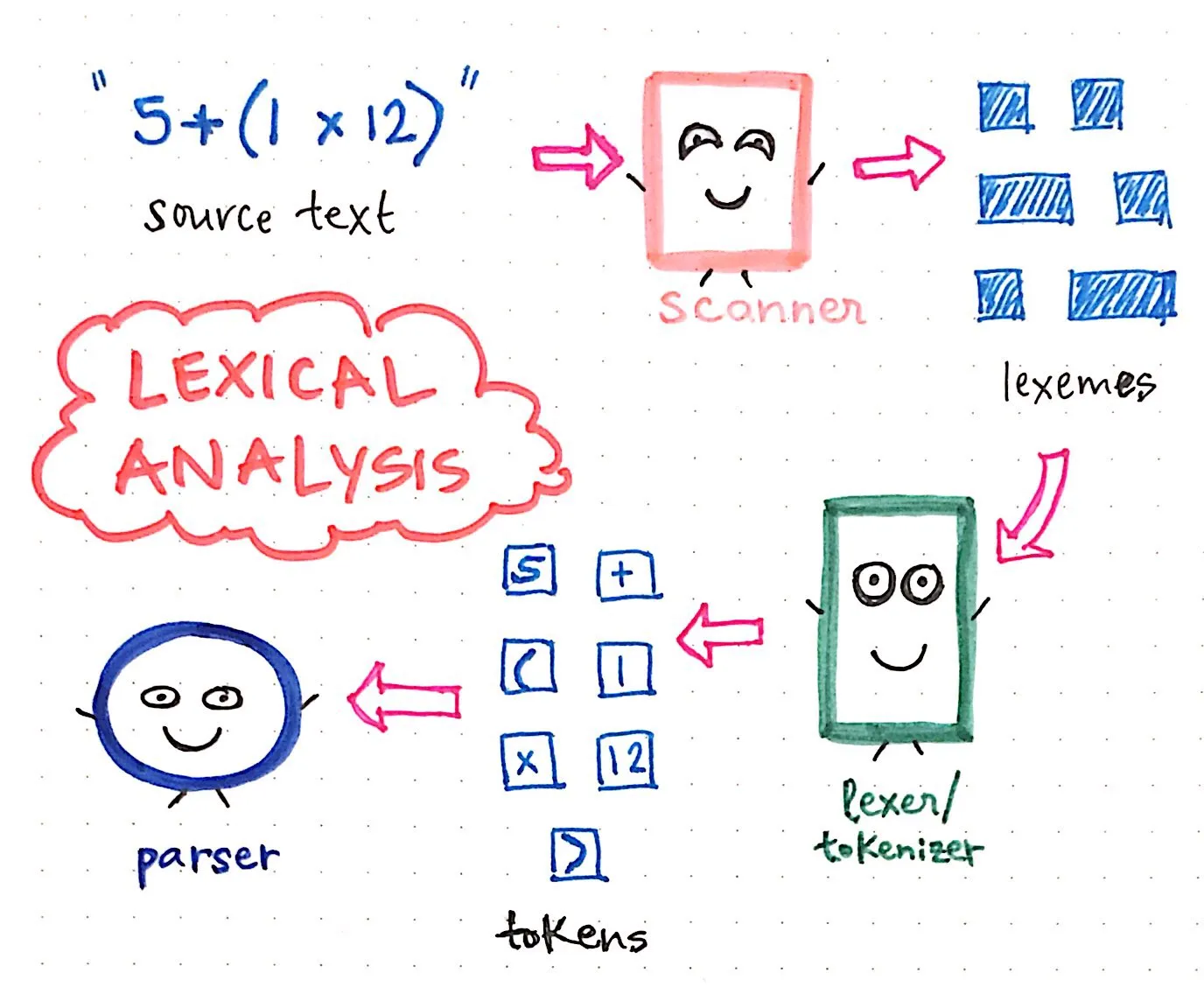
다음과 같이 매우 짧고 달콤한 소스 텍스트가 있다고 가정해 보겠습니다: 5 + (1 x 12).

컴파일 프로세스에서 가장 먼저 일어나는 일은 스캐너가 수행하는 작업인 텍스트 스캐닝(scanning)이며, 이 작업을 통해 텍스트는 어휘(lexemes)라고 하는 가능한 가장 작은 부분으로 나뉩니다. 이 부분은 언어에 구애받지 않으며, 결국 소스 텍스트가 제거된 버전이 남게 됩니다.

다음으로, 이러한 어휘는 렉서/토큰화기로 전달되어 소스 텍스트의 작은 표현을 우리 언어에 맞는 토큰으로 변환합니다. 토큰은 다음과 같이 생깁니다: [5, +, (, 1, x, 12, )]. 스캐너와 토큰화기의 공동 노력이 어휘 분석(lexical analysis)의 컴파일을 구성합니다.

그런 다음 입력이 토큰화되면 그 결과 토큰이 파서에 전달되고, 파서는 소스 텍스트를 가져와 구문 분석 트리를 구축합니다. 아래 그림은 토큰화된 코드가 어떻게 보이는지 구문 분석 트리 형식으로 예시한 것입니다.

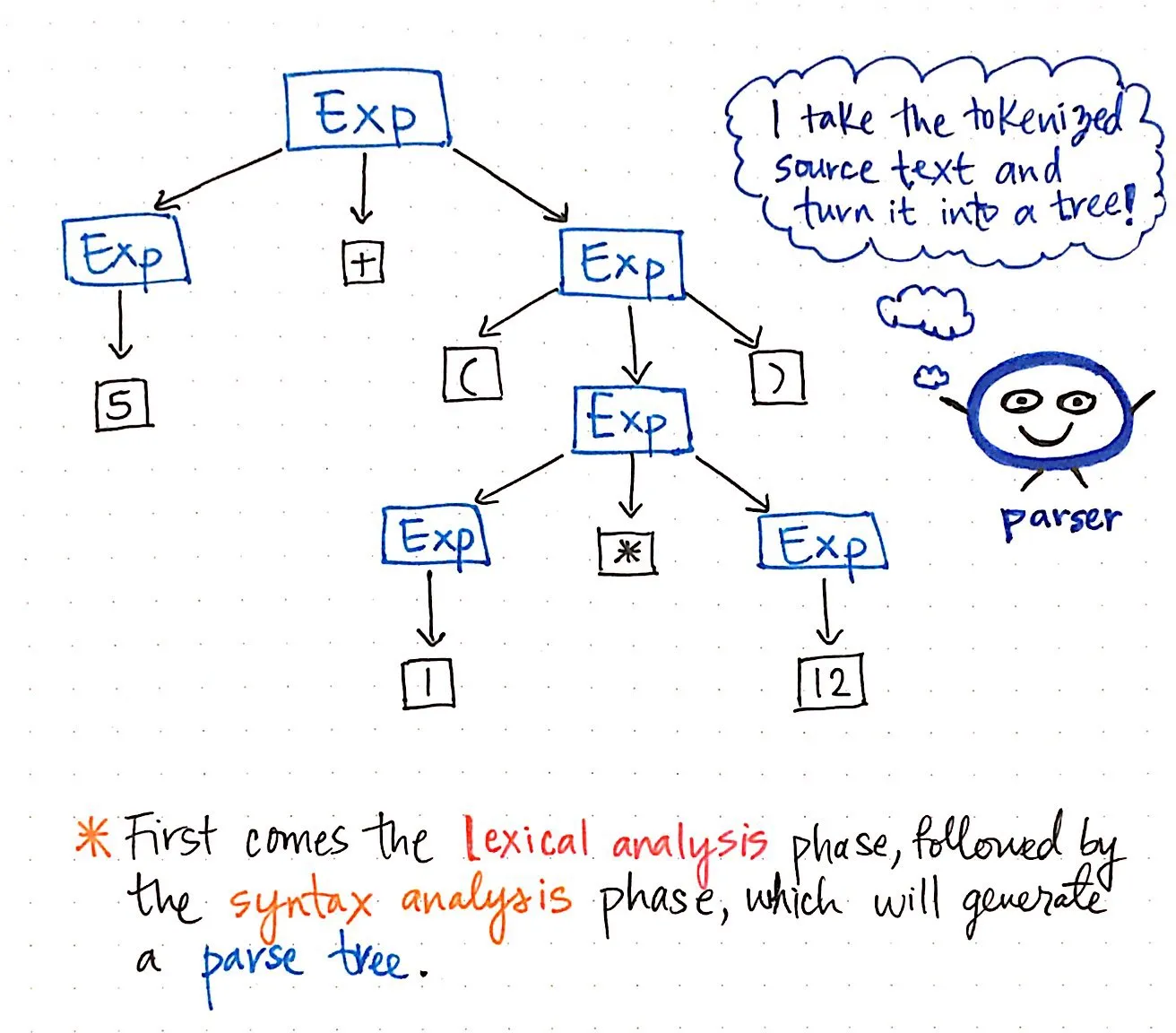
토큰을 구문 분석 트리로 변환하는 작업을 파싱이라고도 하며 구문 분석(syntax analysis) 단계라고 합니다. 구문 분석 단계는 어휘 분석(lexical analysis) 단계에 직접적으로 의존하므로, 컴파일러의 구문 분석기는 토큰화기가 작업을 수행해야만 제 역할을 할 수 있으므로 컴파일 과정에서 항상 어휘 분석이 가장 먼저 이루어져야 합니다!

컴파일러의 각 부분은 텍스트나 파일에서 구문 분석 트리로 코드가 올바르게 변환되도록 서로 의존하는 좋은 친구라고 생각할 수 있습니다.

하지만 원래 질문으로 돌아가서 추상 구문 트리는 이 친구 그룹에 어디에 적합할까요? 이 질문에 답하기 위해서는 먼저 AST의 필요성을 이해하는 것이 도움이 됩니다.

한 트리를 다른 트리로 압축

자, 이제 머릿속에 두 개의 트리가 생겼습니다. 우리는 이미 구문 분석 트리를 가지고 있었고, 또 다른 데이터 구조가 있다는 것을 알게 되었습니다! 그리고 분명히 이 AST 데이터 구조는 단순화된 구문 분석 트리일 뿐입니다. 그렇다면 왜 이것이 필요할까요? 도대체 무슨 소용이 있을까요?

그럼 구문 분석 트리를 살펴볼까요?

우리는 이미 구문 분석 트리가 우리 프로그램을 가장 뚜렷한 부분으로 표현한다는 것을 알고 있으며, 실제로 스캐너와 토큰화기가 표현식을 가장 작은 부분으로 분해하는 중요한 작업을 하는 이유도 바로 여기에 있습니다!

실제로 프로그램을 가장 뚜렷한 부분으로 표현한다는 것은 무엇을 의미할까요?

알고 보면, 때로는 프로그램의 모든 고유한 부분이 실제로 우리에게 항상 유용하지는 않습니다.

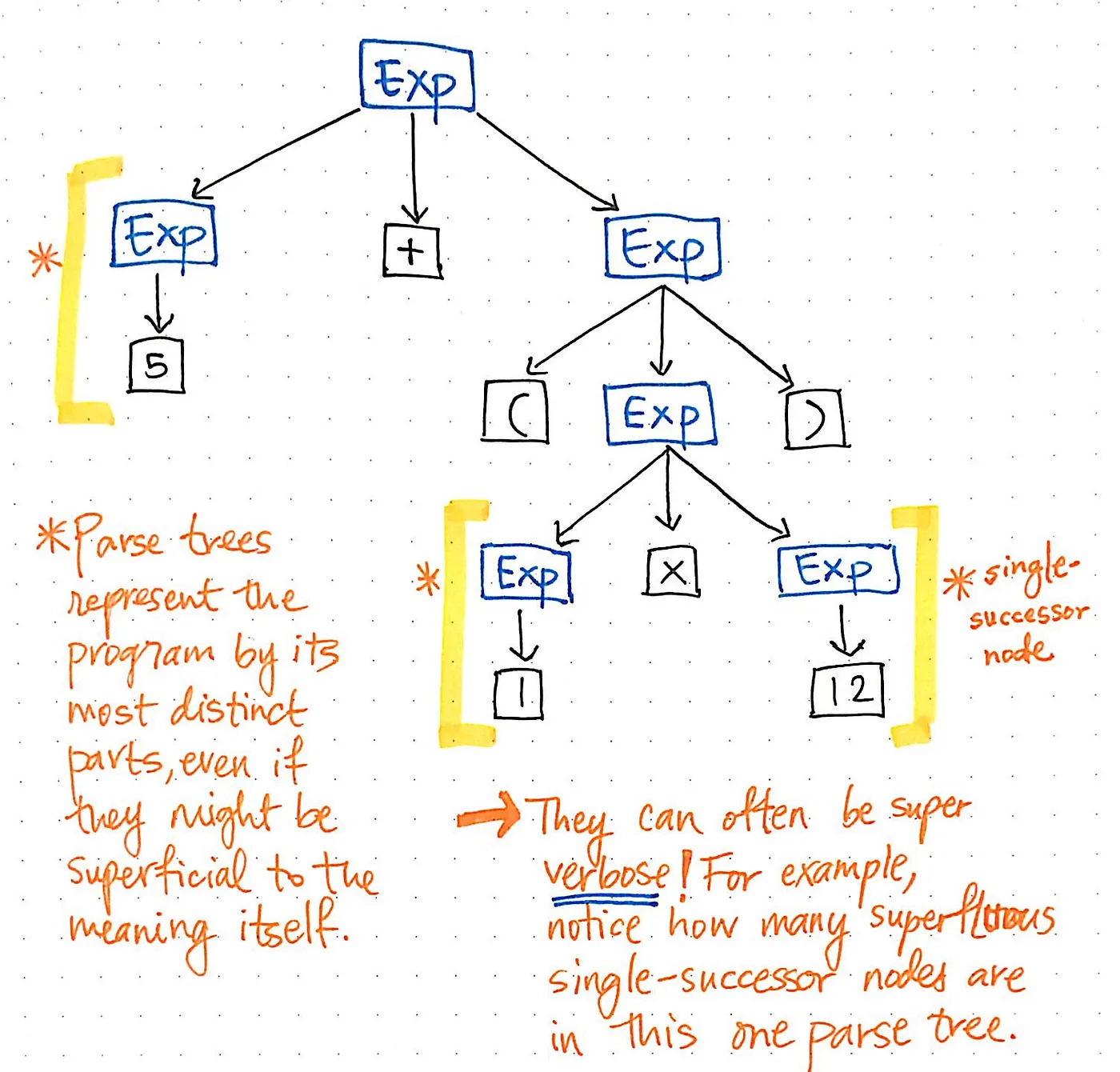
여기에 표시된 그림은 원래 표현식인 5 + (1 x 12)를 파싱트리 형식으로 표현한 것입니다. 이 트리를 비판적인 시각으로 자세히 살펴보면 한 노드에 정확히 하나의 자식이 있는 경우가 몇 가지 있는데, 이러한 노드에서 파생되는 자식 노드가 단 하나(또는 하나의 “후계자”)만 있기 때문에 단일 후계자 노드라고도 합니다.

구문 분석 트리 예제의 경우, 단일 후속 노드에는 5, 1 또는 12와 같은 특정 값의 단일 후속 노드가 있는 Exp(표현식)의 부모 노드가 있습니다. 하지만 여기서 Exp 부모 노드는 실제로 우리에게 어떤 가치도 추가하지 않죠? 토큰/터미널 자식 노드가 포함되어 있는 것은 알 수 있지만 “표현식” 부모 노드에는 관심이 없고, 우리가 정말로 알고 싶은 것은 표현식이 무엇인지뿐입니다.

부모 노드는 트리를 파싱한 후에는 추가 정보를 전혀 제공하지 않습니다. 대신, 우리가 정말로 관심을 두는 것은 단일 자식, 단일 후속 노드입니다. 실제로 이 노드가 우리에게 중요한 정보, 즉 숫자와 값 자체를 제공하는 중요한 노드입니다! 이러한 부모 노드가 우리에게 불필요하다는 사실을 고려하면, 이 구문 분석 트리가 일종의 장황하다는 것이 분명해집니다.

이러한 모든 단일 후속 노드는 우리에게 불필요하며 전혀 도움이 되지 않습니다. 따라서 제거해 봅시다!

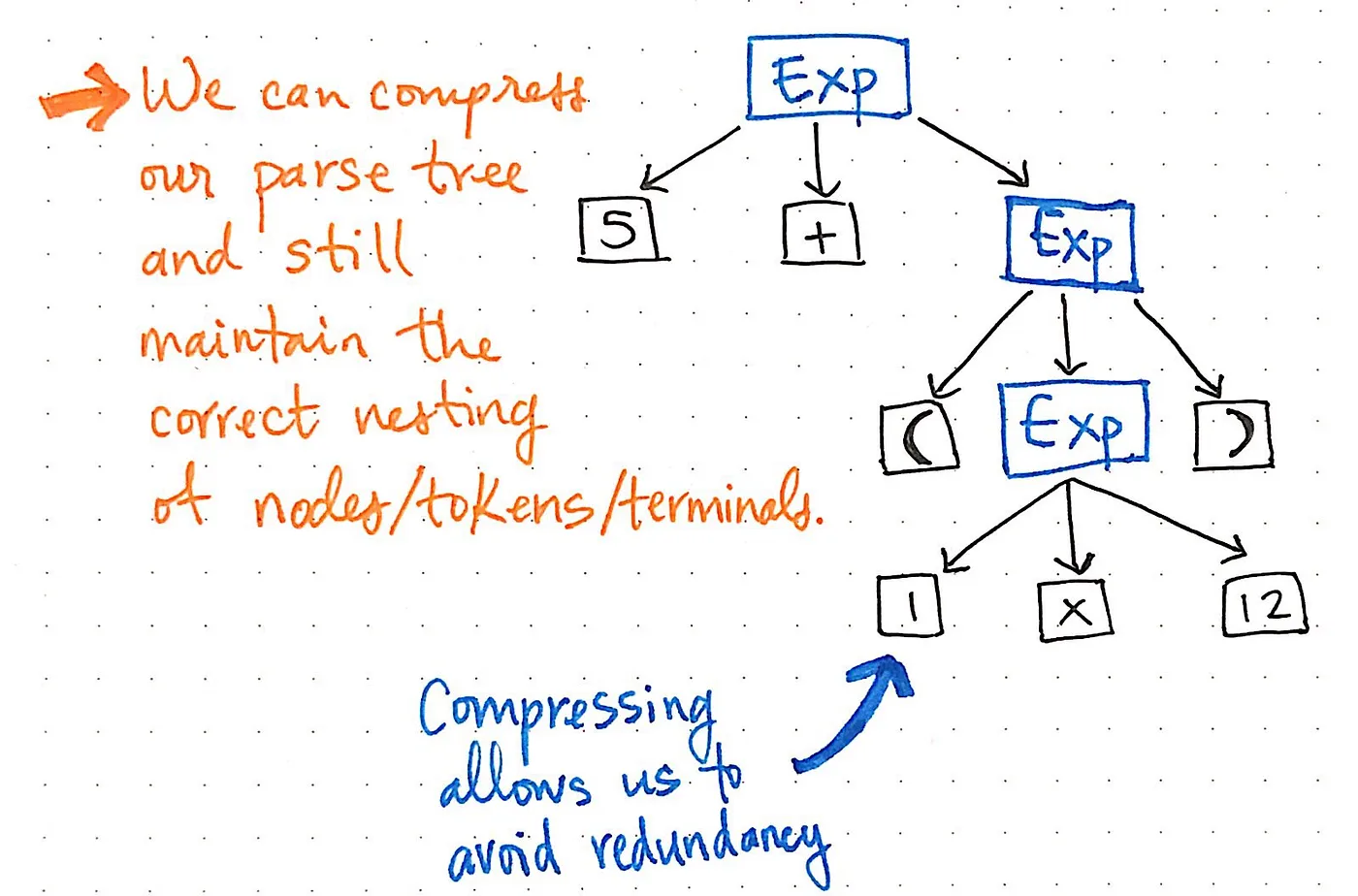
구문 분석 트리에서 단일 후속 노드를 압축하면, 동일한 구조의 더 압축된 버전을 얻게 됩니다. 위의 그림을 보면 이전과 똑같은 중첩을 유지하고 있으며, 노드/토큰/터미널이 여전히 트리 내의 올바른 위치에 표시되고 있음을 알 수 있습니다. 하지만 트리를 조금 더 슬림하게 만들었습니다.

그리고 트리를 좀 더 다듬을 수도 있습니다. 예를 들어, 현재 상태의 구문 분석 트리를 보면 그 안에 거울 구조가 있다는 것을 알 수 있습니다. (1 x 12)의 하위 표현식은 괄호() 안에 중첩되어 있는데, 괄호는 그 자체로 토큰입니다.

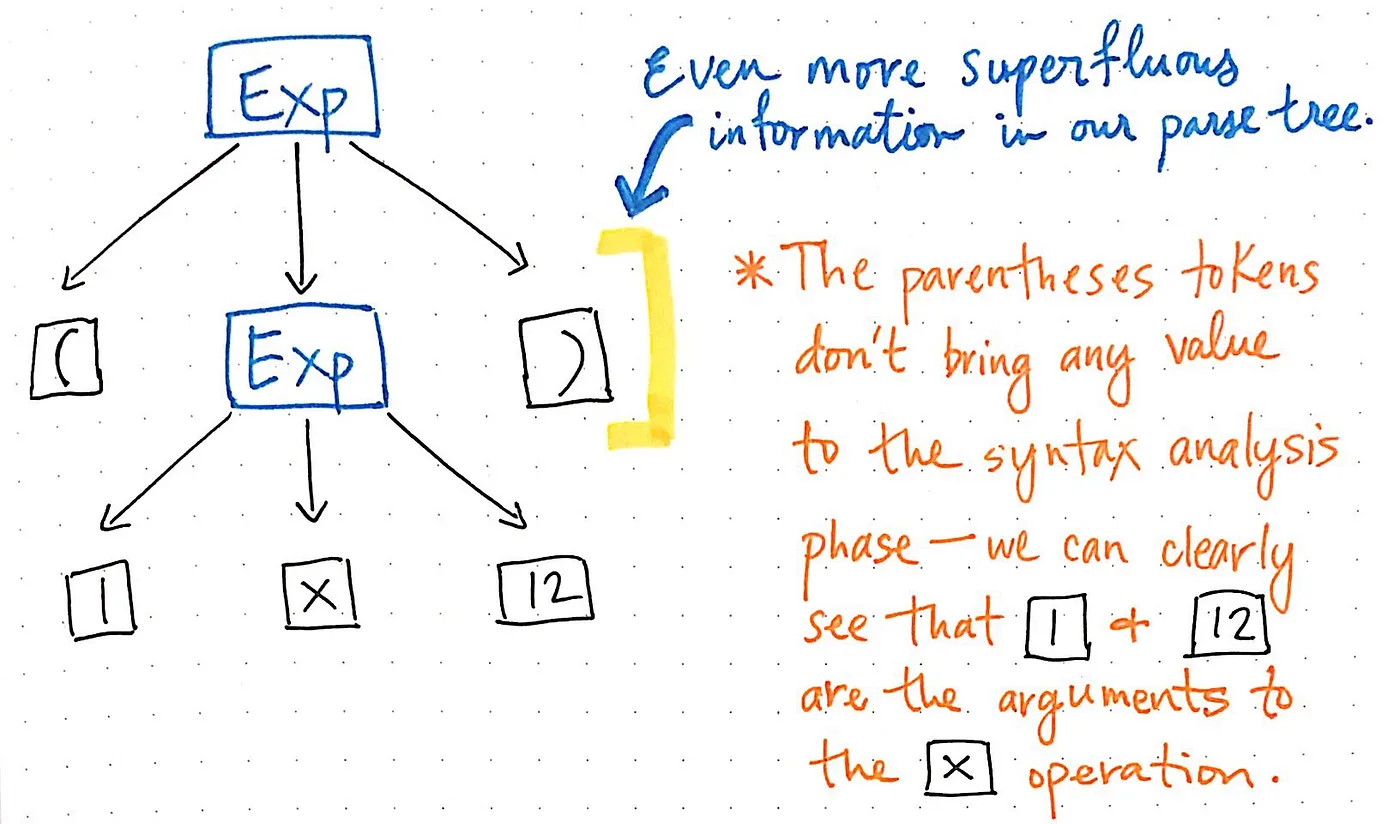
하지만 트리를 완성한 후에는 괄호가 큰 도움이 되지 않습니다. 우리는 이미 1과 12가 곱셈 x 연산에 전달될 인자라는 것을 알고 있으므로 이 시점에서 괄호는 그다지 많은 것을 알려주지 않습니다. 사실, 구문 분석 트리를 더 압축하여 불필요한 리프 노드를 제거할 수도 있습니다.

구문 분석 트리를 압축하고 단순화하여 불필요한 구문 ‘먼지’를 제거하면 이 시점에서 눈에 띄게 달라 보이는 구조를 갖게 됩니다. 사실 이 구조가 바로 새롭고 많은 기대를 모았던 친구인 추상 구문 트리입니다.

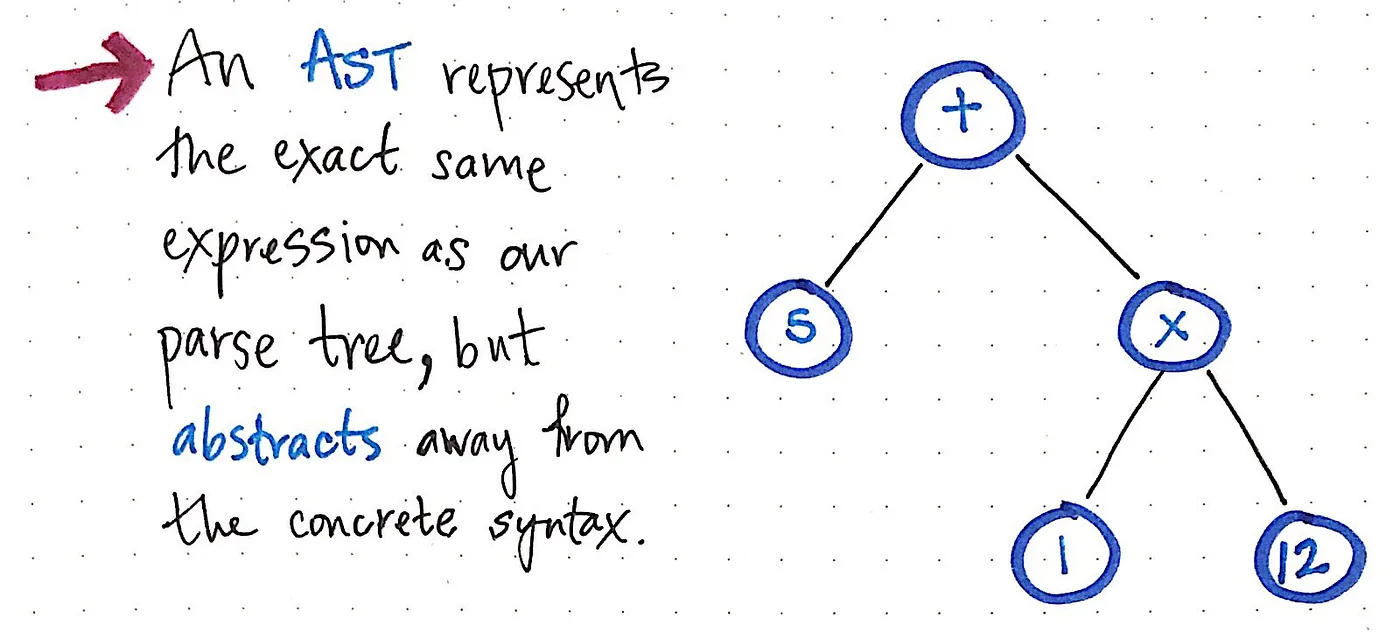
위의 이미지는 구문 분석 트리와 정확히 동일한 표현을 보여줍니다: 5 + (1 x 12). 차이점은 구체적인 구문에서 표현식을 추상화했다는 점입니다. 이 트리에서는 괄호()가 필요하지 않기 때문에 더 이상 괄호가 보이지 않습니다. 마찬가지로 ‘표현식’이 무엇인지 이미 파악했고, 우리에게 정말 중요한 값(예: 숫자 5)을 뽑아낼 수 있기 때문에 Exp와 같은 비종결자가 표시되지 않습니다.

이것이 바로 AST와 CST를 구분하는 요소입니다. 추상 구문 트리는 구문 분석 트리에 포함된 구문 정보의 상당 부분을 무시하고 구문 분석에 사용되는 ‘추가 콘텐츠’를 건너뛴다는 것을 알고 있습니다. 하지만 이제 어떻게 그런 일이 일어나는지 정확히 알 수 있습니다!

이제 자체적인 구문 분석 트리를 압축했으니 AST와 CST를 구분하는 몇 가지 패턴을 훨씬 더 잘 파악할 수 있을 것입니다.

추상 구문 트리가 구문 분석 트리와 시각적으로 구별되는 몇 가지 방법이 있습니다:

1. AST에는 쉼표, 괄호, 세미콜론과 같은 구문 세부 정보가 포함되지 않습니다(물론 언어에 따라 다름).
2. AST는 단일 후속 노드로 표시될 수 있는 것을 축소한 버전을 가지며, 단일 자식이 있는 노드의 “체인”을 포함하지 않습니다.
3. 마지막으로, 모든 연산자 토큰(예: +, -, x, /)은 구문 분석 트리에서 종료되는 리프가 아니라 트리의 내부(부모) 노드가 됩니다.

AST는 정의상 구문 분석 트리의 압축 버전이며 구문 세부 사항이 적기 때문에 시각적으로 항상 구문 분석 트리보다 더 압축적으로 보입니다.

그렇다면 AST가 구문 분석 트리의 압축 버전이라면, 처음부터 구문 분석 트리를 구축할 것이 있어야만 추상 구문 트리를 만들 수 있다는 것은 당연한 이치입니다!

실제로 이것이 추상 구문 트리가 더 큰 컴파일 프로세스에 적합한 방식입니다. AST는 우리가 이미 학습한 구문 분석 트리와 직접 연결되어 있으며, 동시에 AST가 생성되기 전에 렉서에 의존하여 작업을 수행합니다.

추상 구문 트리는 구문 분석 단계의 최종 결과로 생성됩니다. 구문 분석의 주요 ‘주인공’인 구문 분석기는 항상 구문 분석 트리 또는 CST를 생성할 수도 있고 생성하지 않을 수도 있습니다. 컴파일러 자체와 컴파일러의 설계 방식에 따라 구문 분석기는 구문 트리 또는 AST를 바로 생성할 수도 있습니다. 그러나 구문 분석기는 중간에 구문 분석 트리를 생성하든, 생성하기 위해 얼마나 많은 패스를 거쳐야 하든 관계없이 항상 출력으로 AST를 생성합니다.

AST의 해부학

이제 추상 구문 트리가 중요하다는 것을 알았으니(하지만 반드시 어렵지는 않습니다!), 조금 더 자세히 분석해 볼 수 있습니다. AST가 어떻게 구성되는지에 대한 흥미로운 측면은 이 트리의 노드와 관련이 있습니다.

아래 이미지는 추상 구문 트리 내의 단일 노드의 구조를 예시한 것입니다.

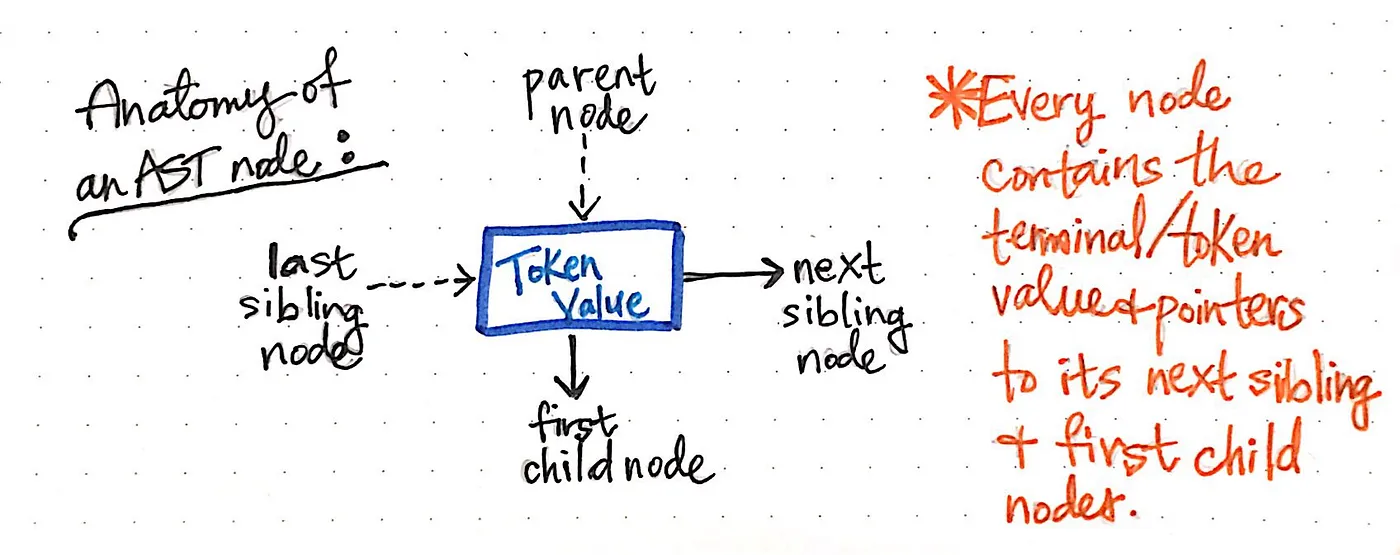
이 노드는 일부 데이터(토큰과 해당 값)를 포함한다는 점에서 이전에 보았던 다른 노드와 유사하다는 것을 알 수 있습니다. 그러나 여기에는 매우 구체적인 포인터도 포함되어 있습니다. AST의 모든 노드는 첫 번째 자식 노드뿐만 아니라 다음 형제 노드에 대한 참조를 포함합니다.

예를 들어, 5 + (1 x 12)라는 간단한 표현식을 아래 그림과 같이 AST의 시각화된 그림으로 구성할 수 있습니다.

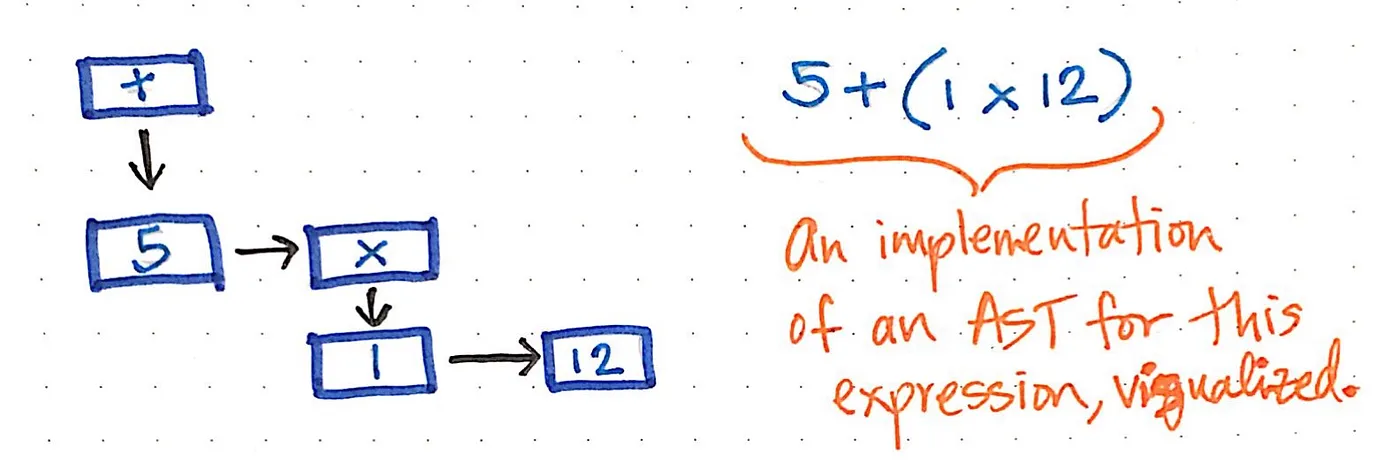
이 AST를 읽고, 트래버스(traversing)하거나, “해석(interpreting)”하는 작업은 트리의 맨 아래 수준에서 시작하여 다시 위로 올라가서 마지막에 값이나 반환 결과를 구축할 수 있다고 상상할 수 있습니다.

또한 시각화를 보완하기 위해 파서 출력의 코딩된 버전을 보는 것도 도움이 될 수 있습니다. 다양한 도구를 활용하고 기존 구문 분석기를 사용하여 구문 분석기를 통해 실행될 때 표현식이 어떻게 보이는지 간단한 예제를 확인할 수 있습니다. 아래는 소스 텍스트인 5 + (1 * 12)를 ECMAScript 파서인 Esprima를 통해 실행한 예시와 그 결과인 추상 구문 트리, 그리고 고유 토큰 목록입니다.

// Using Esprima, a ECMAScript parser written in ECMAScript
// var esprima = require('esprima');
// var program = 'const answer = 42';

// Syntax
{
  "type": "Program",
  "body": [
    {
      "type": "VariableDeclaration",
      "declarations": [
          {
              "type": "VariableDeclarator",
              "id": {
                  "type": "Identifier",
                  "name": "result"
              },
              "init": {
                  "type": "BinaryExpression",
                  "operator": "+",
                  "left": {
                      "type": "Literal",
                      "value": 5,
                      "raw": "5"
                  },
                  "right": {
                      "type": "BinaryExpression",
                      "operator": "*",
                      "left": {
                          "type": "Literal",
                          "value": 1,
                          "raw": "1"
                      },
                      "right": {
                          "type": "Literal",
                          "value": 12,
                          "raw": "12"
                      }
                  }
              }
          }
      ],
      "kind": "var"
    }
  ],
  "sourceType": "script"
}


// Token List
[
  {
    "type": "Keyword",
    "value": "var"
  },
  {
    "type": "Identifier",
    "value": "result"
  },
  {
    "type": "Punctuator",
    "value": "="
  },
  {
    "type": "Numeric",
    "value": "5"
  },
  {
    "type": "Punctuator",
    "value": "+"
  },
  {
    "type": "Punctuator",
    "value": "("
  },
  {
    "type": "Numeric",
    "value": "1"
  },
  {
    "type": "Punctuator",
    "value": "*"
  },
  {
    "type": "Numeric",
    "value": "12"
  },
  {
    "type": "Punctuator",
    "value": ")"
  },
  {
    "type": "Punctuator",
    "value": ";"
  }
]
// A code visualization of our AST expression, using JavaScript.

이 형식에서 중첩된 객체를 보면 트리의 중첩을 확인할 수 있습니다. 1과 12를 포함하는 값은 각각 상위 연산인 ““의 왼쪽과 오른쪽 자식임을 알 수 있습니다. 또한 *곱셈 연산(*)이 전체 표현식 자체의 *오른쪽 하위 트리*를 구성하므로 더 큰 BinaryExpression 객체 내에서 "오른쪽" 키 아래에 중첩되어 있음을 알 수 있습니다. 마찬가지로 5의 값은 더 큰 BinaryExpression 객체의 단일 "왼쪽" 자식입니다.

그러나 추상 구문 트리의 가장 흥미로운 측면은 매우 간결하고 깔끔하지만 항상 쉽게 구축할 수 있는 데이터 구조는 아니라는 사실입니다. 사실, 파서가 다루는 언어에 따라 AST를 구축하는 것은 매우 복잡할 수 있습니다!

대부분의 구문 분석기는 일반적으로 구문 분석 트리(CST)를 구성한 다음 AST 형식으로 변환하는데, 이는 더 많은 단계를 거쳐야 하고 일반적으로 소스 텍스트를 더 많이 통과해야 하지만 때때로 더 쉬울 수 있기 때문입니다. 구문 분석기가 구문 분석하려는 언어의 문법만 알고 있으면 CST를 구축하는 것은 사실 매우 쉽습니다. 토큰이 “중요한” 토큰인지 아닌지를 알아내는 복잡한 작업을 할 필요 없이, 보이는 순서대로 정확히 보고 있는 것을 모두 트리에 뱉어내기만 하면 됩니다.

반면에, 이 모든 작업을 단일 단계 프로세스로 수행하여 추상 구문 트리를 바로 생성하는 구문 분석기도 있습니다.

파서가 토큰을 찾아 올바르게 표현해야 할 뿐만 아니라 어떤 토큰이 중요하고 어떤 토큰이 중요하지 않은지도 결정해야 하기 때문에 AST를 직접 구축하는 것은 까다로울 수 있습니다.

컴파일러 설계에서 AST는 여러 가지 이유로 매우 중요합니다. 구성이 까다로울 수 있고 엉망이 되기 쉽지만 어휘 및 구문 분석 단계가 결합된 마지막 최종 결과물이기 때문입니다! 어휘 및 구문 분석 단계는 흔히 분석 단계 또는 컴파일러의 프론트엔드라고 부르기도 합니다.

추상 구문 트리는 컴파일러 프런트엔드의 ‘최종 프로젝트’라고 생각할 수 있습니다. 프런트엔드에서 마지막으로 보여줘야 하는 것이기 때문에 가장 중요한 부분입니다. 컴파일러가 소스 텍스트를 표현하는 데 궁극적으로 사용하는 데이터 구조가 되기 때문에 이를 기술적으로는 중간 코드 표현(intermediate code representation) 또는 IR이라고 합니다.

추상 구문 트리는 IR의 가장 일반적인 형태이지만 때로는 가장 많은 오해를 받기도 합니다. 하지만 이제 조금 더 잘 이해했으니 이 무서운 구조에 대한 인식을 바꿀 수 있습니다! 이제 조금은 덜 두렵게 느껴지시길 바랍니다.

참고자료

AST에는 다양한 언어로 된 수많은 자료가 있습니다. 특히 더 많은 것을 배우고 싶다면 어디서부터 시작해야 할지 알기 어려울 수 있습니다. 아래는 너무 어렵지 않으면서도 훨씬 더 자세히 설명하는 초보자 친화적인 몇 가지 리소스입니다. Happy asbtracting!

1. The AST vs the Parse Tree, Professor Charles N. Fischer
2. What’s the difference between parse trees and abstract syntax trees?, StackOverflow
3. Abstract vs. Concrete Syntax Trees, Eli Bendersky
4. Abstract Syntax Trees, Professor Stephen A. Edwards
5. Abstract Syntax Trees & Top-Down Parsing, Professor Konstantinos (Kostis) Sagonas
6. Lexical and Syntax Analysis of Programming Languages, Chris Northwood
7. AST Explorer, Felix Kling